3D-Syntax
Allgemein
Die Kurzübersicht der Syntax finden Sie hier: http://server.ibfriedrich.com/download/pdf/de/3D_Syntax_d.pdf
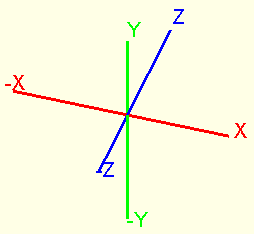
Koordinaten werden in mm angegeben, Dezimaltrennung ist durch einen Punkt möglich. Bei Draufsicht auf die Platine: X (rot) ist die Abszisse und geht positiv nach Osten, negativ nach Westen, Y (grün) ist die Ordinate und geht positiv nach Norden, negativ nach Süden, Z (blau) geht positiv nach oben zum Betrachter, negativ nach unten orthogonal zur X/Y Fläche. Wenn Sie Ihr Objekt um die Z- Achse rotieren wollen, nehmen Sie bitte die [Strg] Taste hinzu.
Koordinatensystem leicht gedreht:
Beispiele:
0,0,0 liegt im Ursprung auf der oberen Oberfläche der Platine.
0,0,0.5 liegt beispielsweise 0,5mm über dem Ursprung auf der Z-Achse
Winkel werden in Grad 0.0 ... 360.0 angegeben, Dezimaltrennung ist durch einen Punkt möglich. In der Platinenebene zählen positive Winkel von der X-Achse zur Y-Achse hin. Senkrecht von der X-Achse zur Z-Achse hin oder von der Y-Achse zur Z-Achse hin.
Beispiele:
0,90
90.0,180.0
Farben als 3-Byte hexadezimaler RGB-Wert.
Beispiele:
- $0000FF - rot
- $00FF00 - grün
- $FF0000 - blau
- $000000 - schwarz
- $FFFFFF - weiß
- $888888 - Pins
- $333333 - IC Körper (DIL, TQFP, ...)
- $443644 - schwarze abgerundete Körper
- $AEAEAE - MetalCan
Die Syntax für einen Körper (=Element) steht immer in einer Zeile, die endlos ist. Die Syntax für ein neues Element beginnt demgemäß einer neuen Zeile. TAB und CR/LF werden überlesen. Alle Angaben, die beim Quader hinter dem Kantradius stehen, gelten als Kommentar und haben keinen Einfluss auf das Modell. Alle Angaben, die bei den anderen Körpern hinter der Farbe stehen, gelten als Kommentar und haben keinen Einfluss auf das Modell.
Um die Grundform eines Objektes zu laden, bedienen Sie sich im 3D-Dialog des Schaltknopfes mit dem Pfeil.
Dieser öffnet Ihnen ein Auswahlmenü, aus dessen erster zeile Sie entsprechende Körper laden können.
Folgende Elemente sind definiert:
Solid (S) (Quader)
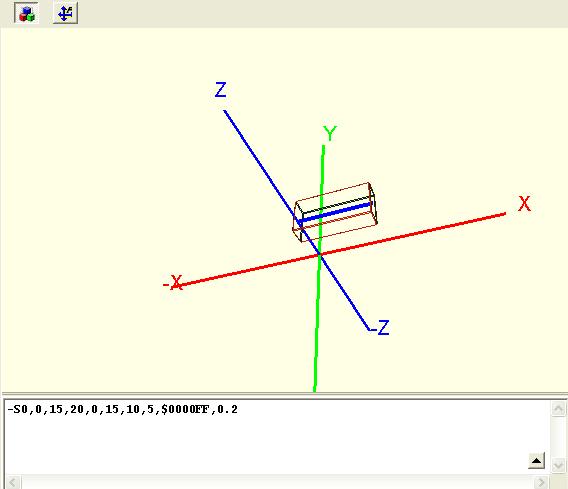
Höhe und Breite sind praktisch eine Verdickung der im Raum liegenden Linie von (X1|Y1|Z1) nach (X2|Y2|Z2). Die Breite liegt immer parallel zur Ebene X-Y. Die Kanten des Quaders sind um den Wert des Kantradius' gebrochen. Für den Sonderfall, dass die Mittenlinie genau in Z-Richtung verläuft, wird die Breite in die X-Richtung gelegt. Mit einem - vor dem S übrigens wird aus dem Solid ein Drahtmodell, was manchmal die Vorstellung erleichtert. Die Mittenlinie wird dann blau dargestellt. Am Drahtmodell können Sie sehen, dass die "Abrundungen" in Wirklichkeit nur Abschrägungen sind, aber die spezielle Beleuchtung vermittelt einen abgerundeten Eindruck.
Syntax:
SX1,Y1,Z1,X2,Y2,Z2,Breite,Höhe,Farbe,Kantenradius.
Beispiel:
-S0,0,15,20,0,15,10,5,$0000FF,0.2 (Wenn Sie das Minuszeichen vor dem S wegnehmen, ist der Quader wieder solid!)
Torus (T) (Kreis/Segment)
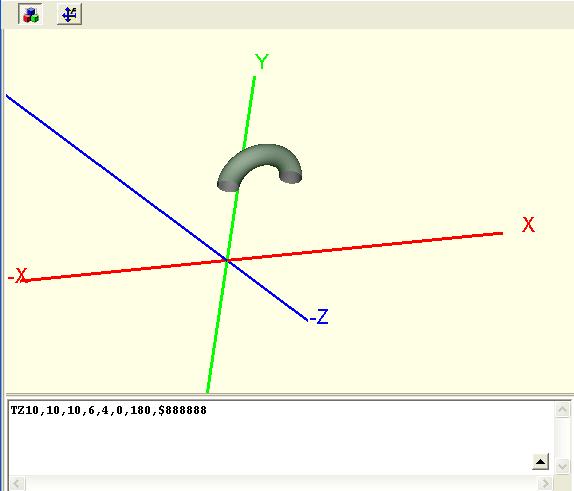
Unter dem Begriff Torus verstehen wir einen Ring oder ein Segment dessen. Er entsteht aus der Rotation eines Kreises um eine Achse. Er hat in der Form eines TZ eine Rotationsachse, die eine Parallele zur Z-Achse darstellt. Pm ist der Mittelpunkt, Radius ist der Radius des Bogens und Dicke der Durchmesser des Kreises, der durch die Rotation zu einem Tubus (Schlauch) wird.
Syntax eines TZ-Torus:
TZXm,Ym,Zm,Radius,Dicke,StartWinkel,EndWinkel,Farbe
Beispiel:
TZ10,10,10,6,4,0,180,$888888
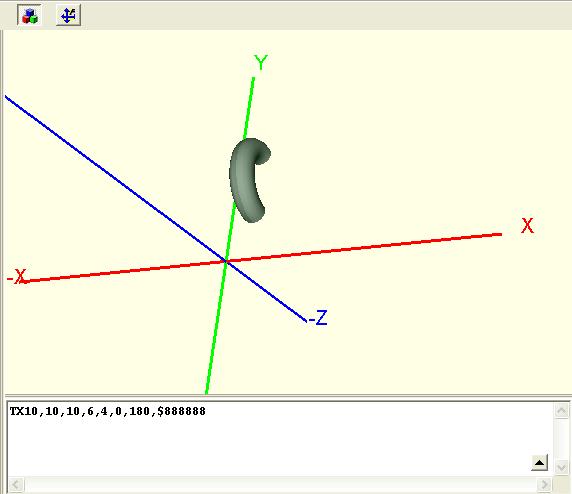
Torus T hat als TX eine Rotationsachse, die eine Parallele zur X-Achse darstellt. Pm ist der Mittelpunkt, Radius der Radius des Bogens und Dicke der Durchmesser des Tubus.
Syntax eines TX-Torus:
TXXm,Ym,Zm,Radius,Dicke,StartWinkel,EndWinkel,Farbe
Beispiel:
TX10,10,10,6,4,0,180,$888888
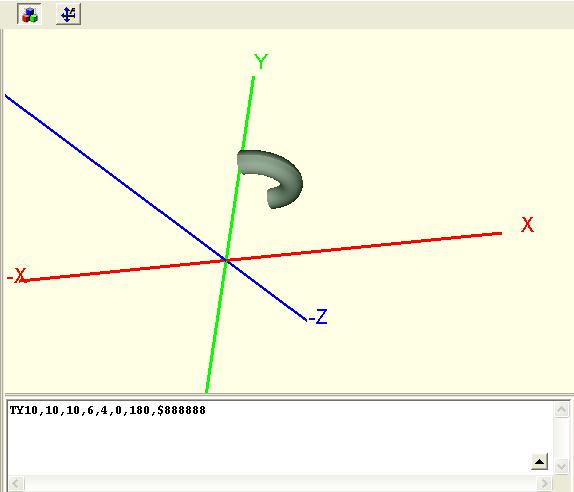
Torus T hat als TY eine Rotationsachse, die eine Parallele zur Y-Achse darstellt. Pm ist der Mittelpunkt, Radius der Radius des Bogens und Dicke der Durchmesser des Tubus. Beachten Sie, dass ein Punkt P immer durch seine XYZ-Koordinaten repräsentiert wird.
Syntax eines TY-Torus:
TYXm,Ym,Zm,Radius,Dicke,StartWinkel,EndWinkel,Farbe
Beispiel:
TY10,10,10,6,4,0,180,$888888
Kugel (Sonderform des Torus)
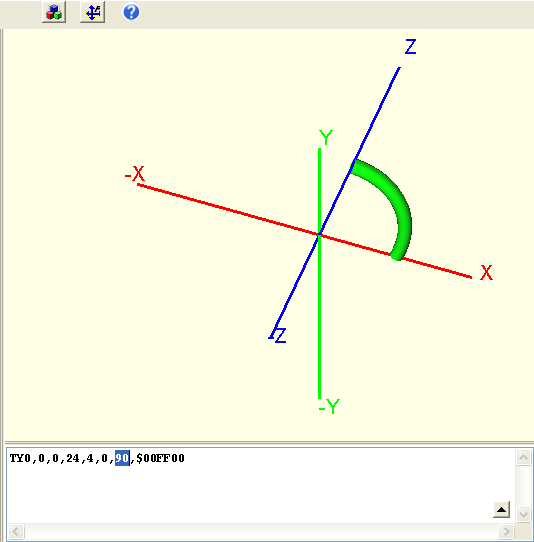
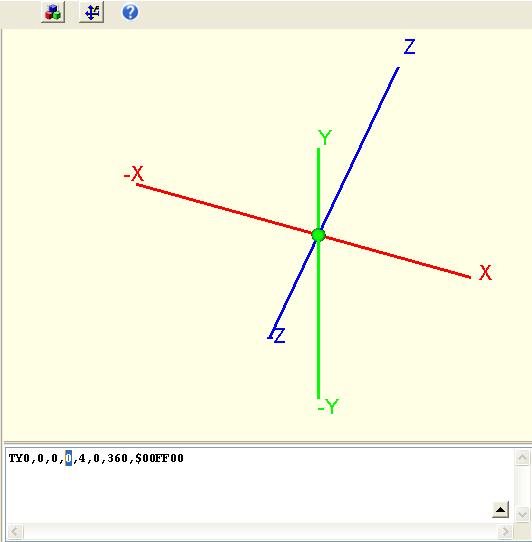
Eine Kugel konstruieren Sie als einen Torus mit Radius=0. Wählen Sie zunächst also die Grundform des Torus aus der Auswahlliste. Folgendes Bild erscheint nach kurzer Mausaktion (M1H im Bild leicht verschieben):
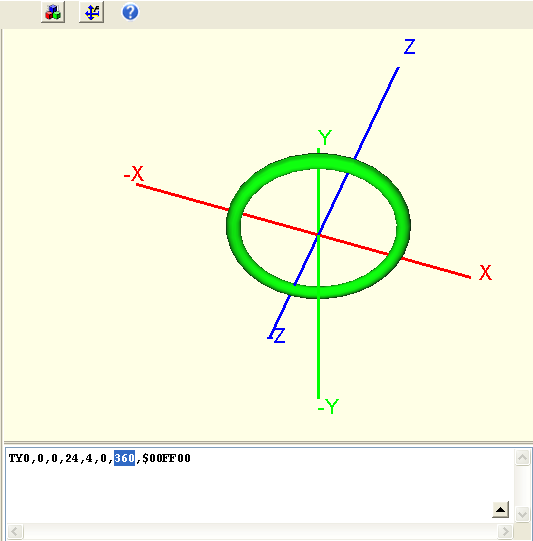
Wir sehen einen Torus als Viertelkreis. Wenn wir die Gradzahl von 90 auf 360 erweitern erhalten wir einen geschlossenen Ring mit Radius 24 mm und Tubus-Stärke von 4mm:
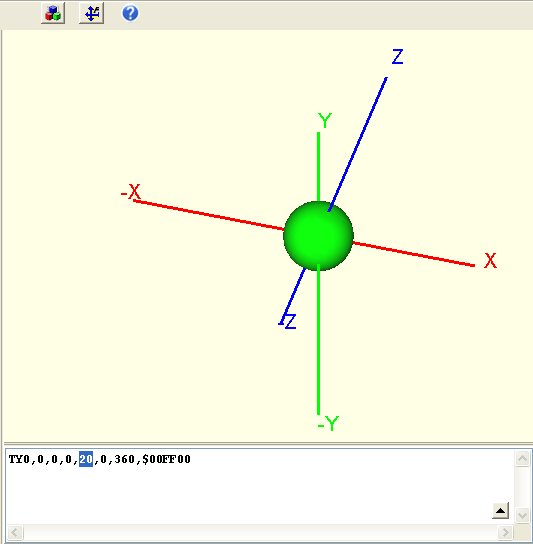
Jetzt setzen wir einfach den Radius von 24 auf 0 und erhalten eine Kugel mit Durchmesser 4mm:
Um den Durchmesser der Kugel zu manipulieren müssen sie also den Wert für die Schlauchdicke aufweiten. Geben Sie also z. B. statt der 4 eine 20 ein, so erhalten Sie eine Kugel mit Durchmesser =20 mm:
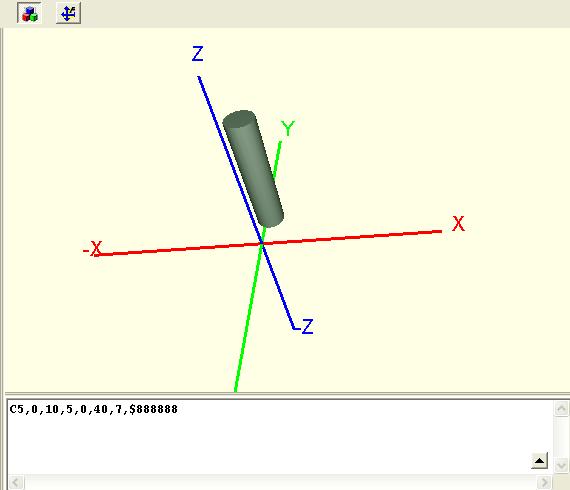
Cylinder (C) (Zylinder)
... mit Deckeln. P1 ist der Startpunkt, P2 der Endpunkt. Geht man von einem bedrahteten Bauteil aus, z. B. dem klassischen Widerstand, ist "Dicke" der Durchmesser des "Drahtes".
Syntax:
CX1,Y1,Z1,X2,Y2,Z2,Dicke,Farbe,Kantenradius
Beispiel:
C5,0,10,5,0,40,7,$888888,0
Ein Zylinder kann auch abgerundete Kanten erhalten:
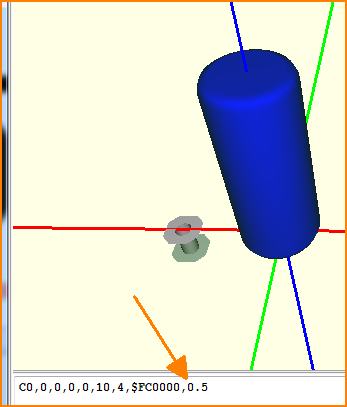
Den Kantenradius tragen Sie nach einem Komma hinter der Farbe ein, s. Pfeil im Bild.
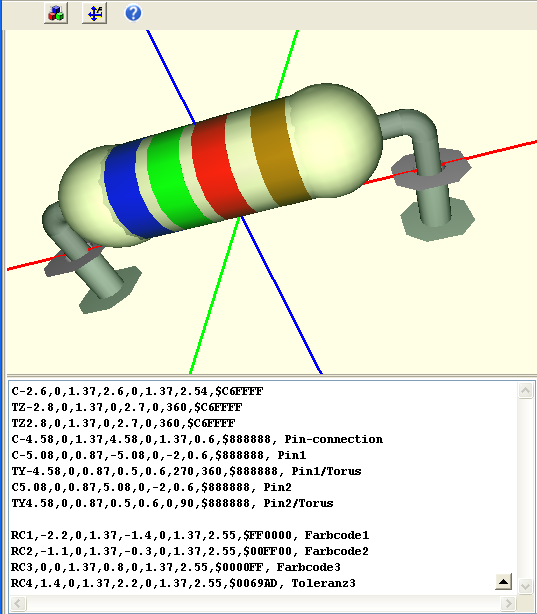
RESISTORCylinder (RC), Farbringe eines Widerstandes
... mit Deckeln. Die erste Zahl ist die Nr. für den Farbring, beginnend von links. P1 ist der Startpunkt, P2 der Endpunkt. Dicke ist der Durchmesser des "Drahtes".
Syntax:
RC1,X1,Y1,Z1,X2,Y2,Z2,Dicke,Farbe,Kommentar
RC2,X1,Y1,Z1,X2,Y2,Z2,Dicke,Farbe,Kommentar
Beispiel:
RC1,-2.2,0,1.37,-1.4,0,1.37,2.55,$FF0000,Farbcode1
RC2,-1.1,0,1.37,-0.3,0,1.37,2.55,$00FF00,Farbcode2
RC3,0,0,1.37,0.8,0,1.37,2.55,$0000FF,Farbcode3
RC4,1.4,0,1.37,2.2,0,1.37,2.55,$0069AD,Toleranz3
Extrudiertes Polygon (E)
...ist immer in der Ebene X-Y und wird in Z-Richtung extrudiert. N ist die Anzahl der Polygonpunkte. Wenn der erste und der letzte Punkt unterschiedlich sind, wird das Polygon geschlossen. Z ist die untere Starthöhe, H die Höhe des Polygons.
Syntax: EN,X1,Y1,,X2,Y2,X3,Y3,...,Z,H,Farbe
Beispiel: E5,9,35,4,7,-14,10,-14,20,-8,13,0,3,$FF0000
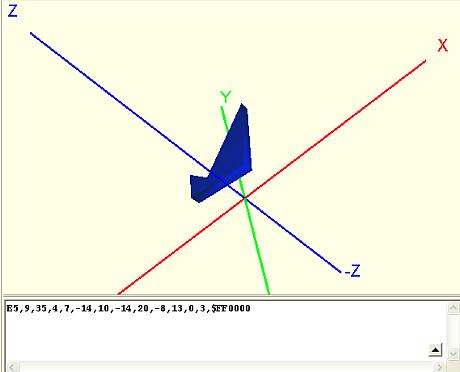
Bild: Ein extrudiertes Polygon (Grundriss in die Höhe gezogen).
Wenn die gesamte 3D-Darstellung genau nur aus dem einen extrudierten Polygon besteht, dann wird der Wert der Höhe H automatisch als Wert der Bauteileigenschaft COMPONENT-HIGHT übernommen. Wenn es weitere 3D-Elemente gibt, dann wird dieser Wert nicht automatisch übernommen.
Text
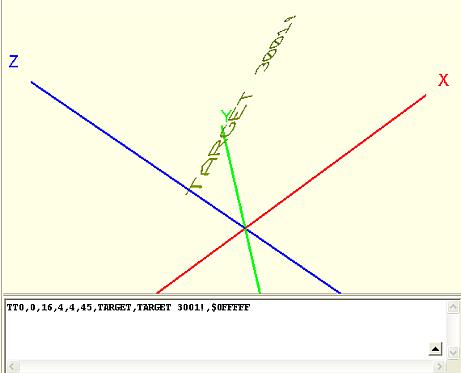
Ein Text, TT oder Text, ist immer parallel zur Oberfläche. Höhe gibt seine Buchstabenhöhe an, Breite seine Buchstabenbreite. Winkel den Winkel in der Ebene X-Y. Fußpunkt ist immer der Punkt vorne unter dem ersten Buchstaben. Die üblichen Platzhalter !Bauteil =Name des Bauteils, !Wert =Wert des Bauteils, !Symbol =Name des (ersten) Symbols in Inhalt werden entsprechend umgesetzt. Oder aber Sie verwenden einen statischen Text, den Sie einfach in dei Syntaxzeile an die entsprechende Stelle schreiben, wie im folgenden Beispiel den Ausdruck TARGET 3001!.
Syntax: TTX,Y,Z,Höhe,Breite,Winkel,Schriftart,Inhalt,Farbe
Beispiel: TT0,0,16,4,4,45,TARGET,TARGET 3001!,$0FFFFF
STEP-File
Eine STEP-Datei wird wie folgt eingebunden:
Syntax: HashSTL,XHashStep,A1,B1,C1,D1,A2,B2,C2,D2,A3,B3,C3,D3,A4,B4,C4,D4,Farbe
Beispiel: X-12345678,87654321,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,$0FFFFF
Die Sequenz beginnt mit "X" und wird gefolgt von zwei internen Hash-Werten für Daten-Container im Projekt. Diese werden automatisch erzeugt, wenn Sie ein STEP-File laden. A1 ... D4 ist eine 4x4 Rotations- und Translationsmatrix. Am Ende steht noch die Farbe. Wenn Sie als Farbe $000000 (schwarz) angeben, dann werden die ggf. vorhandenen Farben des gelesenen STEP-Modells verwendet.